/image%2F0948867%2F20160305%2Fob_9020d2_psi.jpg)
Depuis quelques années, chercheurs, philosophes, architectes, musicologue et mathématiciens se penchent sur les propriétés remarquables du nombre Psi (Ψ). Il est de la même famille que le nombre d’or. Ses propriétés sont analogues. Le nombre d’or est à deux dimensions et permet de qualifier un rapport de proportions dans le plan (il est plus juste de parler de proportion dorée). Quant au nombre radiant, il est à trois dimensions et renvoie à un rapport de proportions entre trois segments. Il s’applique non seulement dans le plan, mais aussi dans l’espace, permettant de qualifier un volume. Moins connu que son grand frère doré, le nombre radiant rayonne aussi fortement. Soucieux des rapports entre musique et architecture, nous avons constaté qu’il comporte une pertinence plus grande en matière musicale et acoustique.
Les deux pionniers de cette investigation sont le mathématicien-polytechnicien Gérard Cordonnier et le moine-architecte-philosophe Hans Van der Laan. Le premier a théorisé et identifié le nombre radiant. Le second lui a donné son enracinement symbolique et philosophique. Dans son ouvrage Le Nombre Plastique, Quinze leçons sur l’ordonnance architectonique, paru en 1960, Van der Laan explique que la filiation de cette découverte remonte aux enseignements de Vitruve. Ce renvoi à l’Antiquité est une manière de consolider la pertinence de sa trouvaille. En effet, dans le De Architectura on trouve de longs développements sur l’importance du respect des rapports de proportions dans les édifices à construire. Ceci est vrai autant pour la proportion dorée que la proportion radiante.
La lecture conjointe des travaux de ces deux chercheurs nous ont permis de mettre en lumière les propriétés remarquables du nombre radiant appliquées à la musique et à l’acoustique. De plus sa symbolique ternaire ouvre des perspectives d’interprétation transversales non négligeables. Van der Laan n’était pas musicien mais il était moine bénédictin, et donc un habitué du chant grégorien. Il a fréquenté Dom Mocquereau à l’abbaye de Solesmes et a été très intéressé par ses recherches sur le Nombre Musical (paru en deux tomes respectivement en 1908 et 1927). Ce dernier considère les aspects de la musique comme subordonnés au rythme du mouvement. « Il n’existe qu’une seule rythmique générale dont les lois fondamentales, établies sur la nature humaine, se retrouvent nécessairement dans toutes les créations artistiques, musicales et littéraires, de tous peuples, dans tous les temps. » (A Mocquereau, Le Nombre musical ou rythmique grégorienne, t.1, p. 26.) Van der Lann sera fasciné par ce travail du musicologue et va faire une transposition au domaine de l’architecture.
Grâce à Gérard Cordonnier que notre ami Claude Genzling nous a fait connaître, nous avons compris la mise en équation du nombre radiant. Mais fondamentalement, comme pour le nombre d’or, le fondement n’est pas ici d’ordre mathématique mais surtout d’ordre métaphysique. Depuis toujours les penseurs ont cherché à concilier l’UN et le MULTIPLE. C’est dans le concept de proportion que l’issue a été trouvée, comme facteur d’harmonie. Qu’il s’agisse des mesures d’un plan d’architecte ou des écarts entre les notes de musique, l’absence de règle d’ordonnancement conduit vite à un désordre et à un chaos. Dès lors que l’on intègre un principe de proportion, cela produit un sentiment de bien être et d’eurythmie. La notion de proportion rapporte donc le MULTIPLE à l’UN par une relation codifiée mathématiquement.
Systématisation du propos
Pour le nombre d’or, la recherche de l’UNITE a conduit à s’intéresser à un rapport étonnant entre deux mesures (ou deux segments) : Dès lors que l’on choisit deux mesures telles que A/B=B/(A+B), on obtient une harmonie remarquable qui a fasciné le Moyen Âge. Cela donne l’équation suivante :
A² + AB = B², soit B²-AB-A² = 0
En divisant l’équation par A², cela donne : (B/A)²- (B/A)-1 =0
Avec l’écriture algébrique moderne : ϕ²- ϕ - 1 = 0
Le nombre d’or (appelé aussi Phi) est la solution de cette équation, soit ϕ = 1,618 (valeur approchée). De plus, à partir de nos trois segments (A, B et A+B) il est possible d’engendrer une série géométrique munie également d’une progression arithmétique : Un+1 = Un-1 + Un= ϕUn. Plus n augmente plus le rapport Un/Un-1 se rapproche de ϕ.
Le nombre radiant, comme nous l’avons dit, possède les mêmes propriétés. La littérature spécialisée ne souligne pas assez qu’il possède lui-aussi une double progression géométrique et arithmétique. C’est pourtant cette double propriété qui a largement contribué à la notoriété du nombre d’or. Grâce à Gérard Cordonnier, ces propriétés du nombre radiant ont été mises en lumière. Il se préparait à publier une étude sur ce sujet, mais il est décédé brutalement sans parvenir à achever son travail… Dans cet article, nous souhaitons nous inscrire dans l’élan de ces deux chercheurs (Van der Laan et Cordonnier) et partager quelques ouvertures dans l’attente d’une future publication.
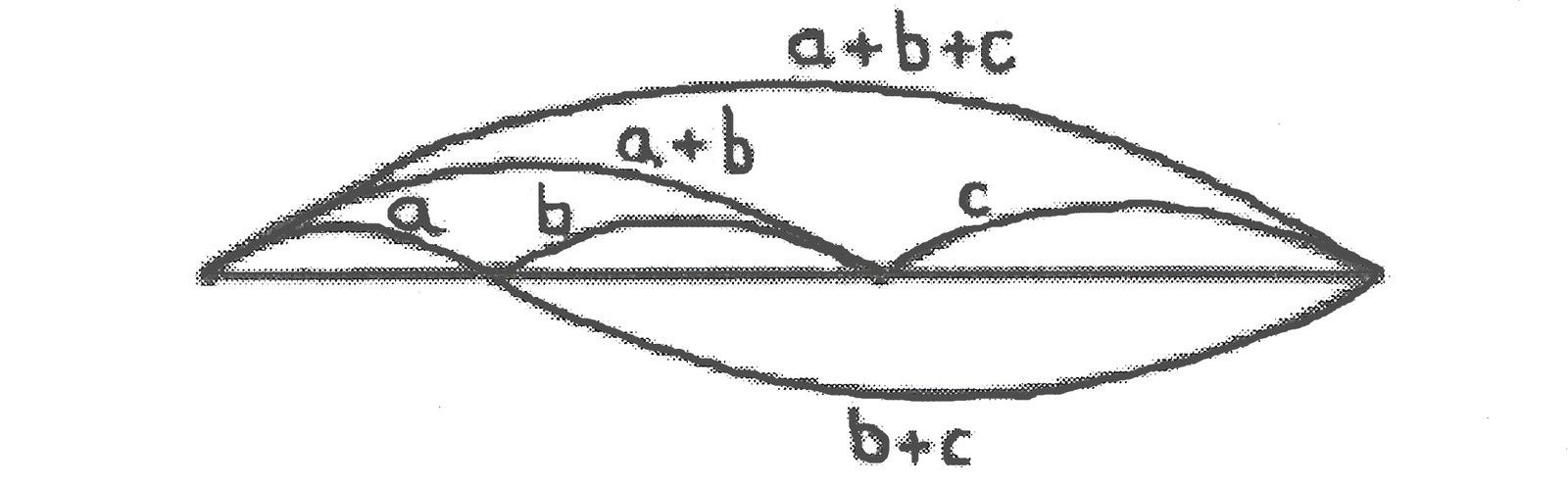
Considérons ici trois segments a, b et c, régit dans des rapports de proportions suivants :
b/a = c/b = (a+b)/c = (b+c)/(a+b) = (a+b+c)/(b+c)
Cela nous donne trois équations : ac = b² et c² = ab + b² et c(b+c) = (a+b)²
On obtient b3 – a²b – a3 = 0, soit (pour a=1) Ψ3 – Ψ – 1 = 0
Ceci correspond à la fois à la suite Un+1 = Un-2 + Un-1 et Un+1 = Ψ Un. Plus n augmente, plus le rapport Un/Un+1 tend vers Ψ. On retrouve bien une série géométrique associée à une progression arithmétique, tout comme pour ϕ. On obtient alors une valeur approchée de Ψ est Ψ = 1,325. Notons qu’Omar Khayyam (1045-1132) avait déjà résolu de manière géométrique la solution de cette équation du 3ème degré en traçant l’intersection d’un demi-cercle et d’une parabole.
Ψ ≈ 4/3 à 1/150ème près.
Selon Claude Genzling, Gérard Cordonnier tenait Ψ pour un nombre aussi important que le nombre d’or, voire même supérieur. On s’en sert effectivement très souvent en architecture et en musique sans pour autant en avoir conscience. Omniprésent dans l’architecture et dans la domotique. La valeur précise de Ψ est 1,3247. Quiconque connaît un peu l’histoire des rapports des nombres à l’architecture sait que la longueur d’un « pied carolingien » est de 0,3248 m. La valeur du pied n’a pas toujours été la même d’une région à l’autre et d’une époque à l’autre. Le plus connu est certainement le « pied romain » (0,2965 m) ; il était employé pour de très nombreuses églises et abbayes romanes. Le pied carolingien a aussi servi de module pour la construction à l’époque médiévale, notoirement pour l’abbaye de Cluny III (on l’appellera ensuite le « pied du roi » et restera en vigueur en France jusqu’en 1799). Nommons « P » cette valeur (P= 0,3248m). On constate avec étonnement que Ψ = 1 + P.
Ceci donne : P = Ψ – 1
Il y a donc une relation mathématiquement très simple entre le nombre radiant et le pied carolingien. On sait aussi qu’avec le pied, la deuxième mesure clé était la coudée qui vaut un pied et demi. Appelons Co la coudée
Co = 3/2 P = 3/2 (Ψ – 1)
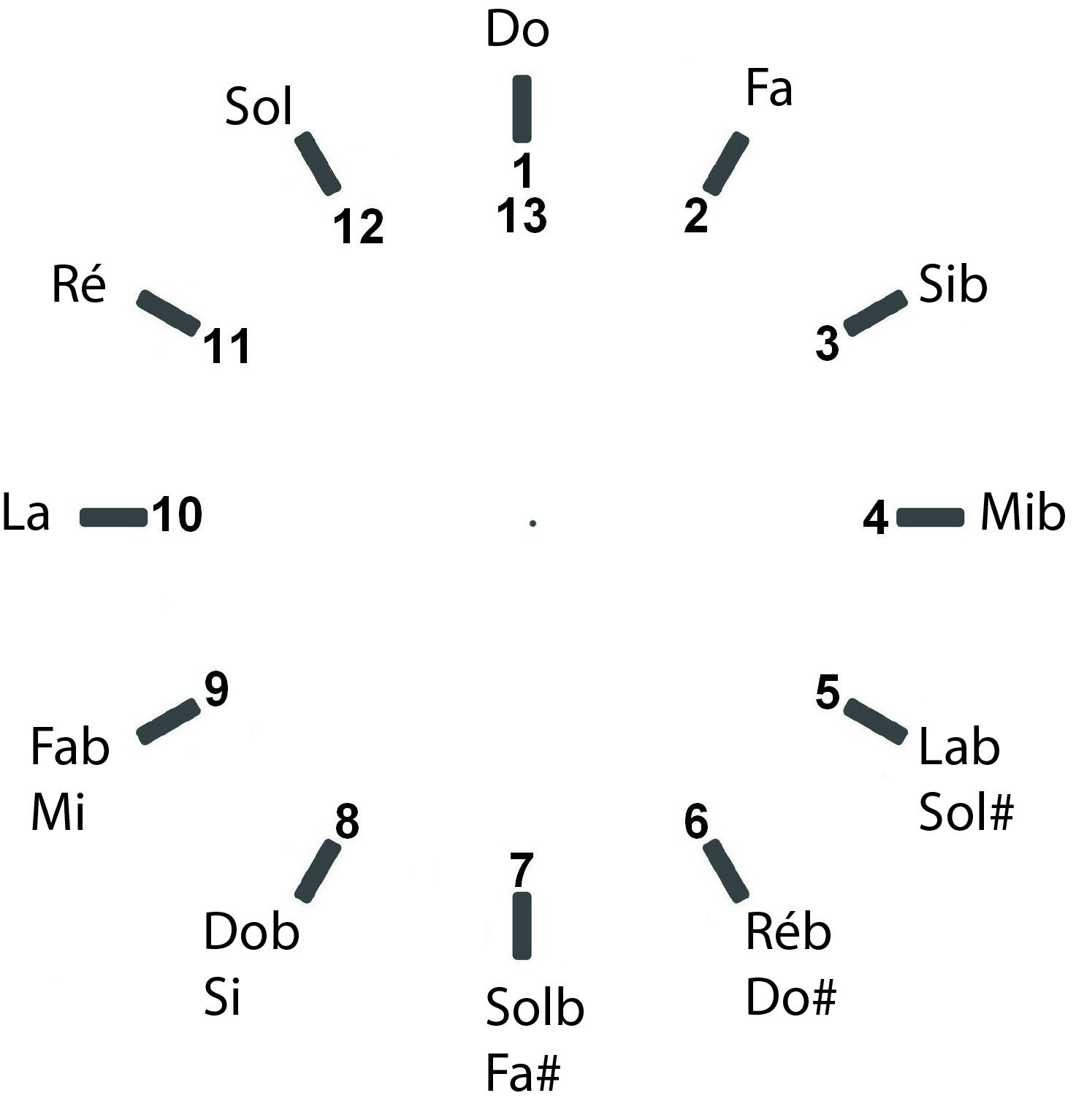
Le nombre radiant ne se retrouva pas seulement en architecture, mais auss en acoustique et en musique. Il est semble parfois caché par le rapport de proportion plus simple de 4/3 (=1,33). C’est sans doute là qu’il faut le chercher. Il correspond au cycle des quartes : On passe effectivement d’une quarte à l’autre par un rapport de fréquence de 4/3. On observe ainsi 12 intervalles avant d’avoir parcouru toutes les notes chromatiques de la gamme. Depuis l’Antiquité, on connaît le cycle des quintes. Mais aujourd’hui le cycle des quartes attire notre attention. Voilà ce que cela donne schématisé :
Fa = Ψ Do (en Hz), et ainsi de suite de quarte en quarte.
Qu’il s’agisse d’une lecture horizontale de la succession de ces notes (mélodie) ou d’une lecture verticale (harmonie), la succession de quartes ou leur superposition dans un accord suscite une ambiance sonore particulière. Ainsi, par exemple, dans l’accord de Do mineur onzième (noté Dom 11) nous retrouvons nos superpositions de quartes : Dom11= Do-Mib-Sol-Sib-Fa
La quinte est l’intervalle naturel fondamental du chant. Son intervalle complémentaire est la quarte. La quinte est le principe « actif », la quarte est l’intervalle résultant pour parvenir à l’octave ; il est donc un intervalle plus « passif ». Pour reprendre (à la suite de Jacques Viret) le schéma extrême-oriental du Yin/Yang (féminin/masculin), la quinte est Yang et la quarte est Yin. « Plus rationnellement, en se référant aux proportions numériques des intervalles musicaux – le chiffre caractéristique étant celui du numérateur –, la quinte (3/2) se relie au nombre trois, impair et masculin ; la quarte (4/3) au nombre quatre, pair et féminin. » (Jacques Viret, Le chant grégorien et la tradition grégorienne, L’Âge d’Homme, 2001, p. 356). Cette lecture doit cependant être clarifiée. Selon nous, la relation quinte / quarte relève davantage du registre de la complémentarité que du dualisme que le Yin/Yang pourrait laisser suggérer. Le rapport masculin / féminin est une complémentarité ; ceci est d’autant plus fort lorsqu’on sait de la tessiture vocale féminine épouse les harmoniques 1 et 2 de la voix masculine. Mais le rapport entre la quarte et la quinte peut aussi être lu comme la rencontre du principe divin (le nombre 3, porté par la quinte) et la réalité du cosmos (le nombre 4, porté par la quarte).
Revenons à l’acoustique avec la question de la note de résonance de l’édifice.
A l’époque médiévale, dès lors que la coudée servait de module de base à toutes les mesures intérieures de l’édifice, elle était aussi une valeur théorique et symbolique clé pour l’acoustique du lieu. En effet, la mise en résonance de l’édifice procède du phénomène des ondes stationnaires. La fréquence d’une onde sonore (F) se calcule de la manière suivante :
F = C / λ, avec C la célérité du son (soit environ 340 m/s à 15°C) et λ la longueur d’onde du son émis.
Pour que F soit une fréquence de résonance, il faut que la longueur d’onde corresponde soit à la coudée de construction (λ = Co), soit au pied de construction (λ = P)
On obtient : F = C / Co = 340 / [3/2 (Ψ – 1)] = 340 / 0,4872 = 697 Hz (soit Fa4)
Ou : F = C / P = 340 / (Ψ – 1) = 340 / 0,3248 = 1047 Hz (soit Do5)
La première équation fait apparaître l’alliance et la conjonction de la quinte et de la quarte. Il en résulte que la fréquence de résonnance associée est soit le Fa (Notons que ce calcul est extrêmement simplifié lorsqu’on pose l’approximation Ψ = 4/3. Notre équation donne F = 680 Hz.), soit le Do. Ainsi la note symbolique de résonance de l’abbatiale de Cluny III était le Fa. C’est une fréquence qui correspond à la tessiture vocale des moines et la hauteur du chant d’un récitatif. Lorsque les moines chantaient sur cette note, l’édifice entrait en résonance. La deuxième note de résonance est en fait la quinte de la première (elle est sa deuxième harmonique). C’est à dire qu’elle entre simultanément en résonance avec la première. Aussi l’utilisation du pied carolingien en architecture (mathématiquement relié à Ψ) permet la conjonction symbolique et acoustique du Yang et du Yin, du principe masculin et féminin. On peut alors se demander où se trouve le principe féminin pour des moines… Il est cependant bien présent de manière symbolique et liturgique : l’Eglise est comprise depuis les écrits de Saint Paul (lettre aux Ephésiens, chap. 5) comme l’épouse du Christ. Cette compréhension nuptiale demeure encore aujourd’hui dans la manière de concevoir architecturalement la construction d’une église.
Nombre radiant et diagramme de Bolt – les dimensions de la pièce idéale acoustiquement
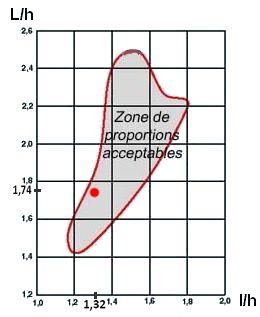
Dans plus de 90% des cas les pièces sont parallélépipédiques. Et les dimensions (longueur, largeur, hauteur) influencent l'acoustique dans celles-ci. Le diagramme de Bolt résulte d’une étude statistique et donne une zone de proportions pertinentes et acceptables. Ce diagramme exprime les ratios identifiés (sur la base de tests empiriques et mathématiques) permettant d'améliorer l'acoustique des salles. Sur ce diagramme vous pouvez lire en abscisse la largeur divisée par la hauteur, et en ordonnées la longueur divisé par la hauteur. Lorsque les deux rapports entrent dans la zone “patatoïde” (délimitée par les pointillés), les proportions sont acceptables.
Vérifions ce qui se passe lorsque l’on utilise le rapport de proportion Ψ. Pour une hauteur sous plafond H donnée, la largeur l = Ψ H et la longueur L = Ψ l = Ψ² H. Appliquées au diagramme de Bolt, on obtient en abscisse x = l/H = Ψ = 1,32 et en ordonnée y = L/H = Ψ² = 1,74. Ainsi, quelque soit la valeur initiale H, lorsqu’on utilise le rapport de proportion du nombre radiant entre les trois dimensions d’une pièce parallélépipédique, la qualité acoustique sera la même. Elle est notifiée par le point rouge sur le diagramme. Elle est bonne et acceptable dans tous les cas. Ainsi, par exemple pour une hauteur sous plafond de 2,40 m, la largeur sera 3,17 m et la longueur 4,18 m. Le nombre radiant permet ainsi de concevoir des volumes acoustiquement très correct et applicable à la taille d’une chambre ou d’un bureau. Remarquons que ceci fonctionne très correctement pour la proportion radiante, mais pas du tout pour la proportion dorée… Pour ce dernier on aurait en abscisse x = 1,62 et en ordonnée y = 2,62. On voit bien que l’on se retrouve alors en dehors de la zone acoustiquement acceptable. Il apparaît indéniable que la proportion radiante comporte des qualités supplémentaires que ne possèdent pas la proportion dorée. Nous l’avons vérifié dans le registre de la musique et de l’acoustique.
Conclusion
Ce bref parcours est la première ébauche d'une étude plus fouillée. Mais ces quelques lignes vous permettront déjà de percevoir quelques enjeux qui transparaissent...
« L’enseignement du nombre plastique trouve son application bien au-delà des limites de l’architecture ; elle nous fait communier à tous les domaines de la création artistique, précisément par ce qui constitue, pour chacun d’eux, leur essence profonde, leur âme. » (Le Nombre Plastique, p. XIV).